[공부 자료 : Must Have 데싸노트의 실전에서 통하는 머신러닝]
# 로지스틱 회귀 (Logistic Regression)
- 로지스틱 회귀
로지스틱 회귀 : 두 가지로 나뉘는 분류 문제(이진 분류)를 다루는 알고리즘
알고리즘의 근간을 선형 회귀 분석에 두고 있어서 선형 회귀 분석과 유사
이름은 회귀이지만, 분류 문제에 사용되는 알고리즘
장점
구현하기 쉽다
계수(기울기)를 사용해 각 변수의 중요성을 쉽게 파악
단점
선형 관계가 아닌 데이터에 대한 예측력이 떨어짐
이진 분류 문제에 선형 회귀가 아닌 로지즈스틱 회귀를 사용해야 하는 이유

- 로지스틱 함수

# 로지스틱 회귀 - 타이타닉 생존자 예측
- 1. 데이터 불러오기
import pandas as pd
file_url = 'https://media.githubusercontent.com/media/musthave-ML10/data_source/main/titanic.csv'
data = pd.read_csv(file_url)- 2. 데이터 확인하기
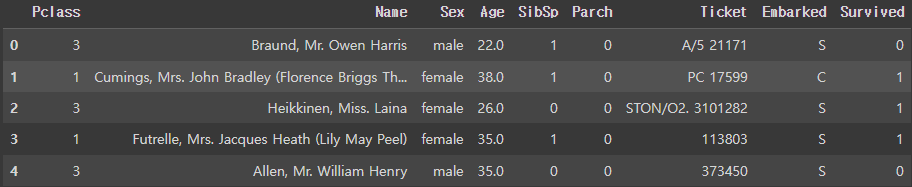
data.head()data.info()
# RangeIndex: 889 entries, 0 to 888
# Data columns (total 9 columns):
# # Column Non-Null Count Dtype
# --- ------ -------------- -----
# 0 Pclass 889 non-null int64
# 1 Name 889 non-null object - 문자형 데이터
# 2 Sex 889 non-null object - 문자형 데이터
# 3 Age 889 non-null float64
# 4 SibSp 889 non-null int64
# 5 Parch 889 non-null int64
# 6 Ticket 889 non-null object - 문자형 데이터
# 7 Embarked 889 non-null object - 문자형 데이터
# 8 Survived 889 non-null int64info( ) 확인 결과 : 결측치는 없지만, 문자형 데이터가 있다
Name, Sex, Ticket, Embarked
data.describe()
describe( ) 확인 결과
Parch의 경우, min / 25% / 50% / 75%는 전부 0인데 max만 6.0
Parch의 대부분 데이터 값은 0이다 (동반 승객 없음)
데이터 확인 - 변수 간 상관관계 분석하기
corr( ) : 변수 간 상관관계 출력
0.2 이하 : 상관관계 낮음
0.2 ~ 0.4 : 낮은 수준의 상관관계
0.4 ~ 0.6 : 중간 수준의 상관관계
0.6 ~ 0.8 : 높은 수준의 상관관계
0.8 이상 : 매우 높은 수준의 상관관계
data.corr()
# 상관관계 값이 클수록 강하다
# Parch(동반 부모/자녀 수)와 SibSp(동반 형제/배우자 수)는 상관관계가 가장 강하다
# 자료형이 object인 변수는 자동으로 빠진다
# Pclass Age SibSp Parch Survived
# Pclass 1.000000 -0.336512 0.081656 0.016824 -0.335549
# Age -0.336512 1.000000 -0.232543 -0.171485 -0.069822
# SibSp 0.081656 -0.232543 1.000000 0.414542 -0.034040
# Parch 0.016824 -0.171485 0.414542 1.000000 0.083151
# Survived -0.335549 -0.069822 -0.034040 0.083151 1.000000heatmap( ) : 히트맵을 통해 변수 간 상관관계 파악
히트맵 색상 배열 검색 : seaborn plaette
import matplotlib.pyplot as plt
import seaborn as sns
sns.heatmap(data.corr())
plt.show()
sns.heatmap(data.corr(), cmap = 'coolwarm') # cmap : 색상 변경
plt.show()
sns.heatmap(data.corr(), cmap = 'coolwarm', vmin = -1, vmax =1, annot = True) # 색상 범위 + 수치
plt.show()
- 3.1. 데이터 전처리 : 더미 변수와 원-핫 인코딩
자료형이 문자(object)인 변수 처리하기
머신러닝 알고리즘에서는 문자열로 된 데이터를 이해하지 못한다
(1) 각 값 (특정 문자) 를 숫자로 대체하기
봄(1), 여름(2), 가을(3), 겨울(4)
선형 모델에 이 방법을 사용할 경우, 숫자가 상대적인 서열로 인식된다
(2) 더미 변수를 사용하기 (원-핫 인코딩)
남자(sex_male = 1, sex_female = 0), 여자(sex_male = 0, sex_female = 1)
sex_male, sex_female 컬럼 : 더미 변수
원-핫 인코딩의 문제점 : 종류가 많을 경우 그만큼 col을 만들어야 한다
# 문자 데이터를 갖는 변수의 고유값 확인하기
data['Name'].nunique() # 889
data['Sex'].nunique() # 2
data['Ticket'].nunique() # 680
data['Embarked'].nunique() # 3drop([col_1, col_2, ...], axis = 1) : DataFrame에서 해당 column을 삭제
Name과 Ticket은 고유값이 너무 많지만, 종속변수에 영향을 주지 않는다 → 삭제
data = data.drop(['Name', 'Ticket'], axis = 1)
data.head()get_dummies(data, columns = [col_1, col_2, ...]) : 원-핫 인코딩
남은 문자 데이터를 갖는 변수(Sex, Embarked)에 대하여 더미 변수를 만든다
pd.get_dummies(data, columns = ['Sex', 'Embarked'])
원-핫 인코딩을 통해 더미 변수를 만들면 해당 변수의 고유값만큼 더미 변수를 만든다
Sex_male을 알면 Sex_female은 자동으로 결정된다
Embarked_Q와 Embarked_S를 알면 Embarekd_C는 자동으로 결정된다
get_dummies(data, columns = [col_1, col_2, ...], drop_first = True) : 첫 번째 더미변수를 자동 삭제
data = pd.get_dummies(data, columns = ['Sex', 'Embarked'], drop_first = True)

- 3.2. 데이터 전처리 : train_test_split
from sklearn.model_selection import train_test_split
X = data.drop('Survived', axis = 1) # data에서 Survived를 뺀게 독립변수
y = data['Survived'] # data의 Survived가 종속변수
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 100)- 4. 모델링
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(X_train, y_train)- 5. 예측하기
pred = model.predict(X_test)
pred
# model.predict() : 예측한 결과를 0.5를 기준으로 1과 0으로 변환
# array([0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1,
# 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0,
# 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0,
# 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1,
# 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0,
# 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1,
# 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0,
# 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0,
# 0, 0])
pred_proba = model.predict_proba(X_test)
pred_proba
# model.predict_proba : 로지스틱 회귀를 통해 진짜로 분석한 결과 [0일 확률, 1일 확률]
# array([[0.92551972, 0.07448028],
# [0.37708123, 0.62291877],
# [0.92277744, 0.07722256],
# [0.45019258, 0.54980742],
# [0.88480543, 0.11519457],
# [0.18748259, 0.81251741],
# [0.90706312, 0.09293688],
# [0.79493606, 0.20506394],
# [0.89888332, 0.10111668],
# [0.3494419 , 0.6505581 ],
# [0.37120425, 0.62879575],
# [0.44706889, 0.55293111],
# [0.64951334, 0.35048666],
# [0.26773463, 0.73226537],
# [0.08265115, 0.91734885],
# [0.88509364, 0.11490636],
# [0.83830721, 0.16169279],
# [0.60594142, 0.39405858],
# [0.67924665, 0.32075335],
# [0.88480543, 0.11519457],
# [0.25098448, 0.74901552],
# [0.25399704, 0.74600296],
# [0.92538289, 0.07461711],
# [0.95908948, 0.04091052],
# [0.05454845, 0.94545155],
# [0.1865422 , 0.8134578 ],
# [0.2913128 , 0.7086872 ],
# [0.90010958, 0.09989042],
# [0.93769962, 0.06230038],
# [0.67181047, 0.32818953],
# [0.07905091, 0.92094909],
# [0.29185877, 0.70814123],
# [0.97121737, 0.02878263],
# [0.95421161, 0.04578839],
# [0.87202375, 0.12797625],
# [0.86750169, 0.13249831],
# [0.35307916, 0.64692084],
# [0.51574066, 0.48425934],
# [0.94423623, 0.05576377],
# [0.6439179 , 0.3560821 ],
# [0.73636615, 0.26363385],
# [0.92551972, 0.07448028],
# [0.44915273, 0.55084727],
# [0.6934977 , 0.3065023 ],
# [0.88067321, 0.11932679],
# [0.94434057, 0.05565943],
# [0.92538289, 0.07461711],
# [0.90010958, 0.09989042],
# [0.93123745, 0.06876255],
# [0.93071254, 0.06928746],
# [0.89212146, 0.10787854],
# [0.86284498, 0.13715502],
# [0.93580721, 0.06419279],
# [0.72282674, 0.27717326],
# [0.88881262, 0.11118738],
# [0.06606613, 0.93393387],
# [0.95106039, 0.04893961],
# [0.58672799, 0.41327201],
# [0.1528808 , 0.8471192 ],
# [0.37120425, 0.62879575],
# [0.87202375, 0.12797625],
# [0.95757652, 0.04242348],
# [0.85311876, 0.14688124],
# [0.25475842, 0.74524158],
# [0.21908075, 0.78091925],
# [0.91967866, 0.08032134],
# [0.24328591, 0.75671409],
# [0.9166796 , 0.0833204 ],
# [0.62400055, 0.37599945],
# [0.95243526, 0.04756474],
# [0.55932145, 0.44067855],
# [0.52829904, 0.47170096],
# [0.15324777, 0.84675223],
# [0.90010958, 0.09989042],
# [0.9914523 , 0.0085477 ],
# [0.90010958, 0.09989042],
# [0.73422093, 0.26577907],
# [0.90010958, 0.09989042],
# [0.65854683, 0.34145317],
# [0.12193454, 0.87806546],
# [0.80595185, 0.19404815],
# [0.84858579, 0.15141421],
# [0.88509364, 0.11490636],
# [0.05676314, 0.94323686],
# [0.03864687, 0.96135313],
# [0.87686787, 0.12313213],
# [0.87373624, 0.12626376],
# [0.03835144, 0.96164856],
# [0.90706312, 0.09293688],
# [0.25998027, 0.74001973],
# [0.24884386, 0.75115614],
# [0.87233933, 0.12766067],
# [0.73422093, 0.26577907],
# [0.88509364, 0.11490636],
# [0.82850745, 0.17149255],
# [0.6439179 , 0.3560821 ],
# [0.86750169, 0.13249831],
# [0.38850399, 0.61149601],
# [0.91357908, 0.08642092],
# [0.92551972, 0.07448028],
# [0.46538808, 0.53461192],
# [0.85002327, 0.14997673],
# [0.91357908, 0.08642092],
# [0.8174557 , 0.1825443 ],
# [0.90010958, 0.09989042],
# [0.63112636, 0.36887364],
# [0.88509364, 0.11490636],
# [0.86750169, 0.13249831],
# [0.21099528, 0.78900472],
# [0.89269732, 0.10730268],
# [0.26773463, 0.73226537],
# [0.34501054, 0.65498946],
# [0.45855693, 0.54144307],
# [0.63007144, 0.36992856],
# [0.86284498, 0.13715502],
# [0.88881262, 0.11118738],
# [0.79858072, 0.20141928],
# [0.43772157, 0.56227843],
# [0.87686787, 0.12313213],
# [0.90010958, 0.09989042],
# [0.85347313, 0.14652687],
# [0.64133848, 0.35866152],
# [0.25971571, 0.74028429],
# [0.28664966, 0.71335034],
# [0.88509364, 0.11490636],
# [0.31660217, 0.68339783],
# [0.2106653 , 0.7893347 ],
# [0.71020326, 0.28979674],
# [0.90066433, 0.09933567],
# [0.56089534, 0.43910466],
# [0.09818447, 0.90181553],
# [0.37120425, 0.62879575],
# [0.79175549, 0.20824451],
# [0.52720453, 0.47279547],
# [0.82878906, 0.17121094],
# [0.91357908, 0.08642092],
# [0.88509364, 0.11490636],
# [0.64951334, 0.35048666],
# [0.427921 , 0.572079 ],
# [0.91395841, 0.08604159],
# [0.0526362 , 0.9473638 ],
# [0.94465497, 0.05534503],
# [0.37120425, 0.62879575],
# [0.19674462, 0.80325538],
# [0.0436084 , 0.9563916 ],
# [0.90010958, 0.09989042],
# [0.77828343, 0.22171657],
# [0.91357908, 0.08642092],
# [0.04189362, 0.95810638],
# [0.73422093, 0.26577907],
# [0.80989304, 0.19010696],
# [0.90010958, 0.09989042],
# [0.87641346, 0.12358654],
# [0.90010958, 0.09989042],
# [0.93324328, 0.06675672],
# [0.37120425, 0.62879575],
# [0.26600736, 0.73399264],
# [0.04879379, 0.95120621],
# [0.46953101, 0.53046899],
# [0.48746283, 0.51253717],
# [0.19927935, 0.80072065],
# [0.68098294, 0.31901706],
# [0.91395841, 0.08604159],
# [0.45795401, 0.54204599],
# [0.52889345, 0.47110655],
# [0.38760663, 0.61239337],
# [0.36748634, 0.63251366],
# [0.13800541, 0.86199459],
# [0.90010958, 0.09989042],
# [0.09303553, 0.90696447],
# [0.05476556, 0.94523444],
# [0.40259165, 0.59740835],
# [0.45855693, 0.54144307],
# [0.95757652, 0.04242348],
# [0.87202375, 0.12797625],
# [0.9524331 , 0.0475669 ],
# [0.90691164, 0.09308836],
# [0.50836634, 0.49163366]])- 6. 평가하기
이진 분류 (binary classification) : Survived는 살았는가/죽었는가
RMSE는 이진 분류의 평가에 적합하지 않다
이진 분류 평가 지표
1. 정확도 (accuracy)
2. 오차 행렬
3. 특이도
4. AUC
5. 정밀도 (precision)
6. 재현율 (recall)
7. F1 Score
8. 민감도
9. 특이도
정확도 : 가장 간단
test set 100개 중 90개를 맞추면 정확도 0.9
from sklearn.metrics import accuracy_score
accuracy_score(y_test, pred)
# 0.7808988764044944- 7. 로지스틱 회귀 모델 분석하기
model.coef_
# array([[-1.18229807, -0.03992439, -0.32137838, 0.00798081, -2.56862996,
# -0.07847763, -0.23534439]])
model.coef_[0]
# array([-1.18229807, -0.03992439, -0.32137838, 0.00798081, -2.56862996,
# -0.07847763, -0.23534439])
pd.Series(model.coef_[0], index = X.columns)
# Pclass -1.182298
# Age -0.039924
# SibSp -0.321378
# Parch 0.007981
# Sex_male -2.568630
# Embarked_Q -0.078478
# Embarked_S -0.235344
# dtype: float64Survived가 1이여야 생존이다
Pclass, Age, SibSp, Sex_male, Embarked_Q, Embarked_S가 낮을수록 생존(1)에 유리하다 (w < 0)
Parch가 높을수록 생존(1)에 유리하다 (w > 0)
로지스틱 회귀에서는 선형 회귀처럼 단순히 계수를 기울기처럼 곱하여 수식을 만들면 안된다
# 피처 엔지니어링
피처 엔지니어링 : 기존의 데이터를 활용하여 더 나은 변수를 만드는 것
더미 변수를 만드는 원-핫 인코딩도 피처 엔지니어링에 포함된다
- 선형 모델의 다중공산성(Multicollinearity) 문제
선형 회귀 분석, 로지스틱 회귀 분석 등 선형 모델에서 발생하는 문제
독립변수 사이에 상관관계가 높을 때 발생
독립변수 A, B와 종속변수 y가 있을 때 A와 B가 모두 y를 양의 방향으로 이끈다면
만약 A와 B의 상관관계가 높을 경우, y가 증가한 이유가 A 때문인지 B 때문인지 명확히 설명할 수 없다
다중공산성 문제를 해결하는 방법
1. 상관관계가 높은 변수 중 하나를 제거
2. 둘을 모두 포괄하는 새로운 변수를 생성
3. PCA(Principal Component Analysis, 주성분 분석)와 같은 차원 축소를 수행
타이타닉 데이터에서 상관관계가 높은 Parch와 SibSp를 새로운 변수로 만들기 : 피처 엔지니어링
Parch : 동반 부모/자식 수
SibSp : 동반 형제/자매/배우자 수
# Parch와 SibSp를 합친, Family col 만들기
data['Family'] = data['SibSp'] + data['Parch']
data.drop(['SibSp', 'Parch'], axis = 1, inplace = True) # SibSp col, Parch col을 삭제하고 data에 반영하기
data.head()
X = data.drop('Survived', axis = 1)
y = data['Survived']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 100)
model = LogisticRegression()
model.fit(X_train, y_train)
pred = model.predict(X_test)
accuracy_score(y_test, pred)
# 0.7921348314606742피처 엔지니어링을 통해 정확도가 0.78에서 0.79로 소폭 상승
'머신러닝' 카테고리의 다른 글
| 07. 지도 학습 (분류) - 나이브 베이즈 : 스팸 메일 분류하기 (0) | 2023.01.25 |
|---|---|
| 06. 지도 학습 (분류, 회귀) - K-최근접 이웃 (KNN) : 와인 등급 예측하기 (0) | 2023.01.22 |
| 04. 지도 학습 (회귀) - 선형회귀 : 보험료 예측하기 (0) | 2023.01.21 |
| 03. Numpy (0) | 2023.01.14 |
| 02. Pandas (0) | 2023.01.13 |


